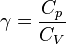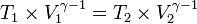Tekanan

Keterangan:
- p: Tekanan (N/m² atau dn/cm²)
- F: Gaya (N atau dn)
- A: Luas alas/penampang (m² atau cm²)
Satuan:
- 1 Pa = 1 N/m² = 10-5 bar = 0,99 x 10-5 atm = 0,752 x 10-2 mmHg atau torr = 0,145 x 10-3 lb/in² (psi)
- 1 torr= 1 mmHg
Tekanan hidrostatis

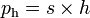
Keterangan:
- ph: Tekanan hidrostatis (N/m² atau dn/cm²)
- h: jarak ke permukaan zat cair (m atau cm)
- s: berat jenis zat cair (N/m³ atau dn/cm³)
- ρ: massa jenis zat cair (kg/m³ atau g/cm³)
- g: gravitasi (m/s² atau cm/s²)
Tekanan mutlak dan tekanan gauge
Tekanan gauge: selisih antara tekanan yang tidak diketahui dengan tekanan udara luar.
Tekanan mutlak = tekanan gauge + tekanan atmosfer
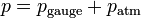
Tekanan mutlak pada kedalaman zat cair
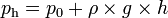
Keterangan:
- p0: tekanan udara luar (1 atm = 76 cmHg = 1,01 x 105 Pa)
Hukum Pascal
Tekanan yang diberikan pada zat cair dalam ruang tertutup akan diteruskan sama besar ke segala arah.

Keterangan:
- F1: Gaya tekan pada pengisap 1
- F2: Gaya tekan pada pengisap 2
- A1: Luas penampang pada pengisap 1
- A2: Luas penampang pada pengisap 2
Jika yang diketahui adalah besar diameternya, maka: 

Gaya apung (Hukum Archimedes)
Gaya apung adalah selisih antara berat benda di udara dengan berat benda dalam zat cair.


Keterangan:
- Fa: gaya apung
- Mf: massa zat cair yang dipindahkan oleh benda
- g: gravitasi bumi
- ρf: massa jenis zat cair
- Vbf: volume benda yang tercelup dalam zat cair
Mengapung, tenggelam, dan melayang
Syarat benda mengapung: 

Syarat benda melayang: 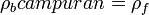
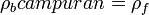
Syarat benda tenggelam: 











 .
.










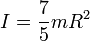


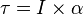


 :Perubahan energi dalam (Joule)
:Perubahan energi dalam (Joule)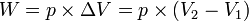
 : Perubahan volume (liter)
: Perubahan volume (liter)



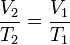




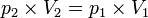


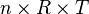 bernilai tetap, maka:
bernilai tetap, maka: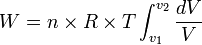

![W = n \times R \times T \times[\ln V_2 - \ln V_1]](http://upload.wikimedia.org/math/0/a/7/0a71834fa480baf975b62a9a64bb7b7d.png)